第十章：排序

# 第十章：排序

# 基本概念

重新排列表中的元素，使表中的元素满足按关键字递增或递减
排序算法的稳定性：两个元素R1，R2，关键字分别是k1，k2，其中k1=k2，R1排在R2前面，如果使用某种排序算法之后，R1仍然在R2前面，则这个排序算法是稳定的，反之不稳定。（注：稳定性并不是衡量一个算法优劣的条件）

# 内部排序

内部排序是指在排序期间元素全部存放在内存中的排序
时空复杂度决定内部排序算法的性能

# 插入排序

每次将一个待排序的序列插入到一个前面已排好的子序列中

# 直接插入排序

步骤：
1. 查找L(i)在L[1, i-1]中的插入位置k
2. 将L[k, i-1]中的所有元素全部后移一个位置
3. 将L(i)复制到L(k)
空间复杂度：O（1）
时间复杂度：O（）
稳定的算法，适用于顺序存储和链式存储

实现：

/* 直接插入排序（从小到大） */
void InsertSort(int arr[], int length)
{
  int i, j, tmp;
  for (i = 1; i < length; i++)
  {
    // 如果待插入元素比有序序列的最后一个元素小，说明需要插入排序
    if(arr[i] < arr[i-1])
    {
      // tmp是待插入的元素
      tmp = arr[i];
      // 将比tmp大的元素全部后移
      for (j = i-1; j >= 0 && arr[j] > tmp; j--)
      {
        arr[j+1] = arr[j];
      }
      // j+1是因为for循环结束之后j--，所以需要重新加回来
      arr[j+1] = tmp;
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 折半插入排序

时间复杂度：折半查找是O（），移动的是O（n），因为外层有for循环，所以总的时间复杂度是O（）
空间复杂度：O（1）
是稳定的算法，适用于顺序存储

/* 折半直接插入排序（从小到大） */
void BInsertSort(int arr[], int n)
{
  int i, j;
  int low, high, mid, tmp;
  for (i = 1; i < n; i++)
  {
    tmp = arr[i];
    // --- start 折半查找插入的位置，最后的hight+1是要插入的位置 ---
    low = 0;
    high = i-1;
    while (low <= high)
    {
      mid = (low + high) / 2;
      if(arr[mid] > tmp)
        high = mid - 1;
      else
        low = mid + 1;
    }
    // --- end 折半查找插入的位置 ---
    // --- start 移动 ---
    for(j = i - 1; j >= high + 1; j--)
      arr[j+1] = arr[j];
    arr[high + 1] = tmp;
    // --- end 移动 ---
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 希尔排序（缩小增量排序）

基本思想：先将排序表分割成d个形如L[i, i+d, i+2d,...,i+kd]的“特殊”子表，分别进行直接插入排序，当整个表中的元素已呈“基本有序时”，再对全体记录进行一次直接插入排序
d的取值：、，直到最后一个
增量gap的取值：gap/3+1
时间复杂度度：O（）
是不稳定的算法，适用于顺序存储

/* 希尔排序 */
void ShellSort(int arr[], int length)
{
  int gap = length;
  int i, j, k;
  do
  {
    // 分组增量
    gap = gap / 3 + 1;
    // 分别对第i组插入排序
    for (i = 0; i < gap; i++)
    {
      // ----start 插入排序 -------
      for (j = i + gap; j < length; j+=gap)
      {
        if(arr[j] < arr[j-gap])
        {
          int tmp = arr[j];
          for (k = j-gap; k >= 0 && arr[k] > tmp; k-=gap)
          {
            arr[k+gap] = arr[k];
          }
          arr[k+gap] = tmp;
        }
      }
      // ----end 插入排序 -------
    }
  } while (gap > 1);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 交换排序

# 冒泡排序

基本思想：假设待排序表长为n，从后往前（从前往后）两两比较相邻元素的值，若为逆序（即A[i-1]>A[i]），则交换他们直到序列比较结束
时间复杂度：O（）
空间复杂度：O（1）
是稳定的算法，适用于顺序存储和链式存储

/* 普通冒泡排序 */
void BubbleSort(int arr[], int length)
{
  for (int i = 0; i < length; i++)
  {
    for (int j = 0; j < length-i-1; j++)
    {
      if(arr[j] > arr[j+1])
      {
        Swap(&arr[j], &arr[j+1]);
      }
    }
  }
}

/* 优化冒泡排序 */
void BubbleSort(int arr[], int n)
{
  int tmp;
  for (int i = 0; i < n-1; i++)
  {
    bool flag = false;
    for (int j = n-1; j > i; j--)
    {
      if(arr[j-1] > arr[j])
      {
        // 交换
        tmp = arr[j-1];
        arr[j-1] = arr[j];
        arr[j] = tmp;
        flag = true;
      }
    }
    if(flag == false)
      return;
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 快速排序

基本思想：在待排序表L[1...n]中任取一个元素pivot作为基准，通过一趟排序将待排序表划分为两部分，左边部分都小于等于pivot，右边部分都大于等于pivot，这两个部分分别又按照新pivot进行划分（递归），最终得到排好序的表。
基本思路：
1. 初始化标记low为第一个元素的位置，high为最后一个元素的位置
2. high向前移动，找到比pivot小的元素
3. low向后移动，找到比pivot大的元素
4. 交换当前两个位置的元素
5. 继续移动标记，执行1、2、3的过程，直到low大于等于high为止
6. 递归
最好、平均时间复杂度：O（）
最好、平均空间复杂度：O（）
最坏时间复杂度：O（）
最坏空间复杂度：O（n）
是不稳定的算法，适用于顺序存储和链式存储

/* 快速排序 */
int Partition(int arr[], int low, int high)
{
  int pivot = arr[low];
  while (low < high)
  {
    // high向前移动，直到找到小于pivot的下标
    while (low < high && arr[high] > pivot)
      high--;
    arr[low] = arr[high];
    // low向后移动，直到找到大于pivot的下标
    while (low < high && arr[low] < pivot)
      low++;
    arr[high] = arr[low];
  }
  arr[low] = pivot;
  return low;
}

void QuickSort(int arr[], int low, int high)
{
  if(low < high)
  {
    int pivotpos = Partition(arr, low, high);
    // 左边部分递归
    QuickSort(arr, low, pivotpos-1);
    // 右边部分递归
    QuickSort(arr, pivotpos+1, high);
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 选择排序

# 直接选择排序

基本思想：每一趟后面n-i+1（i=1，2，，n-1）个待排序元素中选取关键字最小的元素，作为有序子序列的第i个元素，直到n-1趟做完，待排序元素只剩1个
时间复杂度：O（），时间复杂度与初始序列无关
空间复杂度：O（1）
是不稳定的算法，适用于顺序存储和链式存储

/* 选择排序 */
void SelectSort(int arr[], int n)
{
  int tmp;
  for (int i = 0; i < n - 1; i++)
  {
    for (int j = i + 1; j < n; j++)
    {
      if(arr[j] < arr[i])
      {
        // 交换
        tmp = arr[j];
        arr[j] = arr[i];
        arr[i] = tmp;
      }
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 堆排序

堆：n个关键字序列L[1...n]称为堆，当且仅当该序列满足（1 <= i <= |n/2|）：
1. 若L(i)<=L(2i),且L(i)<=L(2i+1)，则称为小根堆
2. 若L(i)>=L(2i),且L(i)>=L(2i+1)，则称为大根堆

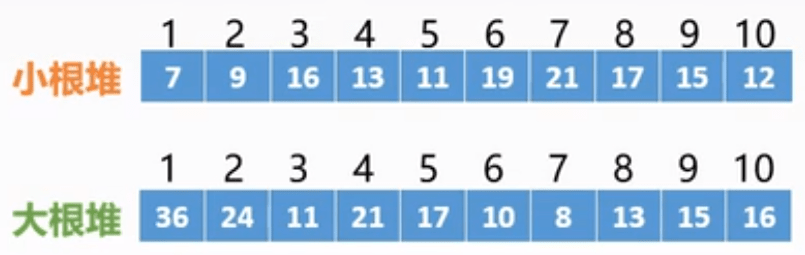
在排序过程中将L[1...n]视为一棵完全二叉树的顺序存储结构

堆的初始化（大根堆）：

时间复杂度：O（n）

void BuildMaxHeap(int arr[], int len)
{
    for(int i = len / 2; i > 0; i--)
        AdjustDown(arr, i, len);
}
void AdjustDown(int arr[], int k, int len)
{
    int tmp = arr[k];
    for(int i == 2 * k; i <= len; i *= 2)
    {
        if(i < len && arr[i] < arr[i+1])
            i++;
        if(tmp >= arr[i])
            break;
        else
        {
            tmp = arr[i];
            k = i;
        }
    }
    arr[k] = tmp;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

堆排序

void HeapSort(int arr[], int len)
{
	BuildMaxHeap(arr, len);
    int tmp;
    for(int i = len; i > 1; i--)
    {
        tmp = arr[i];
        arr[i] = arr[1];
        arr[1] = tmp;
        AdjustDown(arr, 1, i-1);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

堆排序的时间复杂度是：O（）
堆排序的空间复杂度是：O（）
是一个不稳定的算法，适用于顺序存储和链式存储

# 归并排序

# 外部排序

外部排序是指排序期间元素无法全部同时存放在内存中，必须在排序的过程中根据要求不断地在内、外存之间移动

#数据结构 #考研

上次更新: 2020/11/13, 18:11:00

← 第九章：查找