第三章：线性表

定义

线性表是具有相同数据类型的n（n>0）个数据元素的有限序列，其中n为表长，当n=0时线性表为空表，若用L命名线性表，一般表示为：

• 几个概念：
  • 第i个元素在线性表成为位序
  • 是表头元素，是表尾元素
  • 第一个元素无前驱，最后一个元素无后继，其他元素有且只有一个前驱和后继

ADT 线性表（List）
Data
	线性表的数据对象集合为{a1,a2,a3,...,an}，每个元素的类型均为DataType。其中，除第一个元素a1外，每一个元素有且只有一个直接前驱元素，除最后一个元素an外，每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
Operation
	InitList(*L)：初始化操作，建立一个空表L。
	ListEmpty(L)：若线性表为空，返回true，否则返回false。
	ClearList(*L)：将线性表清空。
	GetElem(L,i,*e)：将线性表L中的第i个位置元素值返回给e
	LocateELem(L,e)：查找下标
	ListInsert(*L,i,e)：在线性表L第i个位置插入e
	ListDelete(*L,i,*e)：删除线性表L中第i个位置的元素，并把值返回给e
	ListLength(L)：获取线性表L的元素的个数
endADT

顺序表

顺序表是用顺序存储的方式实现线性表，顺序存储是把逻辑上相邻的元素存储在物理位置也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。

• 存、读：O（1）
• 插入、删除：O（n）

定义

1. 静态分配：存储空间MaxSize是静态的，不可改变的

/* 顺序表实现---静态分配 */
#include <stdio.h>
#define MaxSize 10
/*
  定义顺序表结构
*/
typedef struct
{
	int data[MaxSize];
	int length;
}SqList;
/*
  初始化顺序表
*/
void InitList(SqList *L)
{
	// 顺序表初始长度为0
	L->length = 0;
}
/*
  主函数入口
*/
int main()
{
   	SqList L;
	InitList(&L);
	for(int i = 0; i < MaxSize; i++)
	{
		printf("data[%d]=%d\n", i, L.data[i]);
	}
   	return 0;
}

2. 动态分配：容量大小是可变的

/* 顺序表实现---动态分配 */
#include <stdlib.h>
#include <stdio.h>

#define InitSize 10  // 默认的最大长度

/*
  定义顺序表结构
*/
typedef struct 
{
  int *data;  // 数组指针
  int MaxSize;  // 顺序表的最大容量
  int length;  // 顺序表的当前长度
} SeqList;

/*
  初始化顺序表
*/
void InitList(SeqList *L)
{
  L->data = (int *)malloc(InitSize * sizeof(int));
  L->length = 0;
  L->MaxSize = InitSize;
}

/*
  扩大顺序表容量
*/
void IncreaseSize(SeqList *L, int len)
{
  // 定义指针p指向原来的data内存空间，这里原来的内存空间大小是10
  int *p = L->data;
  // 把data的指针改为指向新的内存空间，这里的新空间大小是15,
  L->data = (int *)malloc((L->MaxSize + len) * sizeof(int));
  // 把旧空间的数据（p）复制到新空间（data）
  for (int i = 0; i < L->length; i++)
  {
    L->data[i] = p[i];
  }
  // 更改容量大小
  L->MaxSize = L->MaxSize + len;
  // 把旧空间释放掉
  free(p);
}

/*
  主函数入口
*/
int main()
{
  SeqList L;
  InitList(&L);
  printf("旧空间大小%d\n", L.MaxSize);
  IncreaseSize(&L, 5);
  printf("新空间大小%d\n", L.MaxSize);
  return 0;
}

插入

/* 顺序表 -- 插入 */
#include <stdio.h>
#define MaxSize 10
/*
  定义顺序表结构
*/
typedef struct
{
	int data[MaxSize];
	int length;
}SqList;
/*
  初始化顺序表
*/
void InitList(SqList *L)
{
	L->length = 6;
}
/*
  插入：在第i个元素之前插入e
*/
void ListInsert(SqList *L, int i, int e)
{
  for (int j = L->length; j >= i; j--)
  {
    L->data[j] = L->data[j-1];
  }
  L->data[i-1] = e;
  L->length = L->length + 1;
}
/*
  主函数入口
*/
int main()
{
  SqList L;
	InitList(&L);
  ListInsert(&L, 3, 3);
  for (int i = 0; i < L.length; i++)
  {
    printf("a[%d]=%d\n", i, L.data[i]);
  }
  
  return 0;
}

• 时间复杂度分析（i是插入的位置，n是表长L.length）：
  1. 最好情况：新元素插入到表尾，不需要移动元素，i=n+1，循环0次，时间复杂度为O（1）
  2. 最坏情况：新元素插入到表头，需要将原有的n个元素全向后移动，i=1，循环n次，时间复杂度为O（n）
  3. 平均情况：i=1,2,3,...,n+1的概率都是，i=1时循环n次，i=2时循环n-1次，...， i=n+1时循环0次，所以平均循环次数为：，即O（n/2），即O（n）

删除

/* 顺序表 -- 删除 */
#include <stdio.h>
#include <stdbool.h>
#define MaxSize 10
/*
  定义顺序表结构
*/
typedef struct
{
	int data[MaxSize];
	int length;
}SqList;
/*
  初始化顺序表
*/
void InitList(SqList *L)
{
	L->length = MaxSize;
  for (int i = 0; i < L->length; i++)
  {
    L->data[i] = i;
  }
  
}
/*
  删除：删除第i个的元素，并将它的值返回给e
*/
bool ListDelete(SqList *L, int i, int *e)
{
  if(i < 1 || i > L->length)
  {
    return false;
  }
  *e = L->data[i-1];
  for (int j = i-1; j < L->length; j++)
  {
    L->data[j] = L->data[j+1];
  }
  L->length--;
  return true;
}
/*
  主函数入口
*/
int main()
{
  SqList L;
	InitList(&L);
  int e = -1;
  if(ListDelete(&L, 7, &e))
  {
    for (int i = 0; i < L.length; i++)
    {
      printf("a[%d]=%d\n", i, L.data[i]);
    }
    printf("删除的值：%d", e);
  }
  else
  {
    printf("删除错误\n");
  }
  
  return 0;
}

• 时间复杂度分析（i是删除的位置，n是表长L.length）：
  1. 最好情况：删除表尾元素，不需要移动元素，i=n，循环0次，时间复杂度为O（1）
  2. 最坏情况：删除表头元素，需要将原有的n-1个元素全向后移动，i=1，循环n-1次，时间复杂度为O（n）
  3. 平均情况：i=1,2,3,...,n+1的概率都是，i=1时循环n-1次，i=2时循环n-2次，...， i=n时循环0次，所以平均循环次数为：，即O（(n-1)/2），即O（n）

按位查找

/* 顺序表 -- 按位查找 */
#include <stdio.h>
#include <stdbool.h>
#define MaxSize 10
/*
  定义顺序表结构
*/
typedef struct
{
	int data[MaxSize];
	int length;
}SqList;
/*
  初始化顺序表
*/
void InitList(SqList *L)
{
	L->length = MaxSize;
  for (int i = 0; i < L->length; i++)
  {
    L->data[i] = i;
  }
  
}
/*
  查找：查找第i个的元素，并将它的值返回给e
*/
bool GetElem(SqList *L, int i, int *e)
{
  if(i < 1 || i > L->length)
  {
    return false;
  }
  *e = L->data[i-1];
  return true;
}
/*
  主函数入口
*/
int main()
{
  SqList L;
	InitList(&L);
  int e = -1;
  int i = 11;
  if(GetElem(&L, i, &e))
  {
    printf("第%d个元素的值为：%d", i, e);
  }
  else
  {
    printf("查找错误\n");
  }
  return 0;
}

按值查找

/*
  顺序表 -- 按值查找
*/
#include <stdlib.h>
#include <stdio.h>

#define InitSize 10  // 默认的最大长度

/*
  定义顺序表结构
*/
typedef struct 
{
  int *data;  // 数组指针
  int MaxSize;  // 顺序表的最大容量
  int length;  // 顺序表的当前长度
} SeqList;

/*
  初始化顺序表
*/
void InitList(SeqList *L)
{
  L->data = (int *)malloc(InitSize * sizeof(int));
  L->length = 7;
  // 插入一些测试数据
  for (int i = 0; i < L->length; i++)
  {
    L->data[i] = i;
  }
  L->MaxSize = InitSize;
}

/*
  按值查找
*/
int LocationElem(SeqList *L, int e)
{
  for (int i = 0; i < L->length; i++)
  {
    if (L->data[i] == e)
    {
      return i+1;
    }
  }
  return -1;
}

/*
  主函数入口
*/
int main()
{
  SeqList L;
  InitList(&L);
  int e = 1;
  int i = LocationElem(&L, e);
  printf("%d在顺序表的位置是：%d", e, i);
  return 0;
}

• 时间复杂度分析（i是查找的位置，n是表长L.length）：
  1. 最好情况：查找表头元素，i=1，循环1次，时间复杂度为O（1）
  2. 最坏情况：删除表尾元素，i=n，循环n次，时间复杂度为O（n）
  3. 平均情况：i=1,2,3,...,n+1的概率都是，i=1时循环1次，i=2时循环2次，...， i=n时循环n次，所以平均循环次数为：，即O（(n+1)/2），即O（n）

优缺点

• 优点：
  1. 无须为表示元素之间的逻辑关系而增加额外的存储空间
  2. 可以快速地读存取表中任一位置的元素
• 缺点：
  1. 插入和删除需要移动大量元素
  2. 当线性表长度变化大的时候，难以缺点存储空间的容量
  3. 造成存储空间的“碎片”

链表

链表分为：单链表、双链表、循环链表、静态链表

单链表（带头结点）

相关概念

• 数据域：存储数据元素信息的域
• 指针域：存储后继位置的域
• 结点：数据域和指针与组成的元素的存储映像
• 单链表：链表的每个结点只包含一指针域
• 头指针：链表的第一个结点的存储位置
• 头结点：单链表的第一个结点前的结点，它的数据域一般存储如线性表长度等附加信息，不存储实际数据

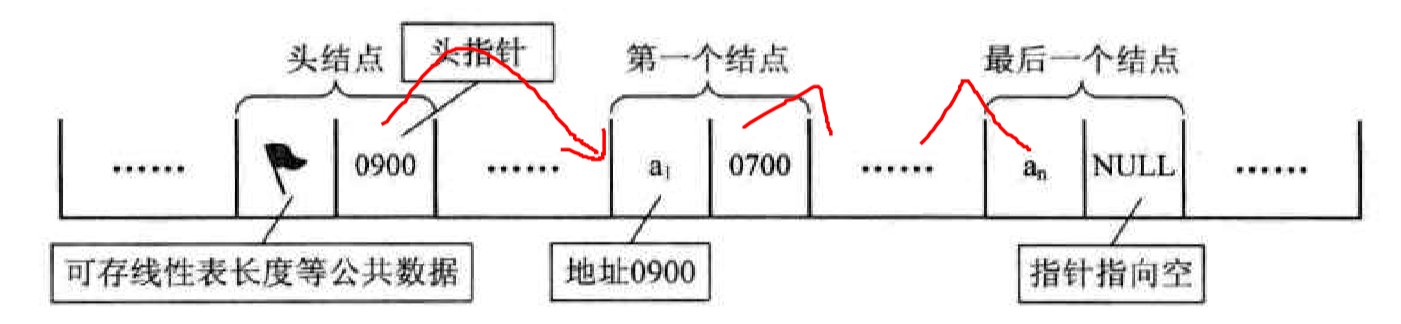
定义

/* 结点的结构体 */
struct LNode
{
  int data;
  struct LNode *next;
};
typedef struct LNode LNode;
typedef struct LNode *LinkList;

初始化

/* 初始化链表 */
void InitList(LinkList *L)
{
  *L = (LinkList)malloc(sizeof(LNode));
  if(*L == NULL)
  {
    printf("分配结点失败\n");
    exit(-1);
  }
  (*L)->next = NULL;
  printf("初始化列表完成\n");
}

是否为空

/* 判断链表是否为空 */
void ListEmpty(LinkList L)
{
  if(L->next == NULL)
    printf("链表为空\n");
  else
    printf("链表不为空\n");
}

获取长度

/* 获取链表长度 */
int ListLength(LinkList L)
{
  int j = 0;
  LNode *p = L->next;
  while (p)
  {
    j++;
    p = p->next;
  }
  printf("链表的长度是%d\n", j);
  return j;
}

按位查找

/* 按位查找 */
void GetElem(LinkList L, int i, int *e)
{
  int j = 0;
  LNode *p = L;
  while (p && j < i)
  {
    j++;
    p = p->next;
  }
  if(!p || i < 1)
    exit(0);
  *e = p->data;
  printf("查找到的值为；%d\n", *e);
}

按值查找

/* 按值查找 */
int LocateElem(LinkList L, int e)
{
  int j = 0;
  LNode * p = L -> next;
  while (p)
  {
    j++;
    if(p->data == e)
    {
      printf("查找到的下标为；%d\n", j);
      return j;
    }
    p = p->next;
  }
  return -1;
}

按位插入

/* 
  按位插入：在第i个位置插入e
  思路：
    1. 找到第i-1个节点p
    2. 声明一个新节点s
    3. s的data设为e
    4. s的next设为p的next
    5. p的next设为s
*/
int ListInsert(LinkList L, int i, int e)
{
  if(i < 1)
    exit(-1);
  LNode *p = L;
  int j = 0;
  while (p != NULL && j < i-1)
  {
    p = p->next;
    j++;
  }
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));

  s->data = e;
  s->next = p->next;
  p->next = s;

  return 0;
}

前插

/* 
  指定结点的前插
  思路：
    1. 声明一个新节点s
    2. s的next设为指定结点的next
    3. s的data设为指定结点的data
    4. 指定结点的next设为s
    5. 指定结点的data设为e
*/
int InsertPriorNode(LNode *p, int e)
{
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));
  s->next = p->next;
  s->data = p->data;
  p->next = s;
  p->data = e;
  return 0;
}

后插

/* 
  指定结点的后插
  思路：
    1. 声明一个新节点s
    2. s的data设为e
    3. s的next设为指定结点的next
    4. 指定结点的next设为s
*/
int InsertNextNode(LNode *p, int e)
{
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));
  s->data = e;
  s->next = p->next;
  p->next = s;
  return 0;
}

按位删除

/*
  按位删除
  思路：
    1. 找到i-1结p
    2. 令新结点q指向p的next（即指向要删除的结点）
    3. p->next=q-next（跨过要删除的结点）
*/
int ListDelete(LinkList *L, int i, int *e)
{
  int j = 0;
  LNode * p = *L;
  LNode * q;
  if(*L == NULL)
    exit(0);
  if(i==1)
  {
    q = p->next;
    free(*L);
    *L = q;
  }
  else
  {
    while (p != NULL && j < i - 1)
    {
      j++;
      p = p->next;
    }
    if(p == NULL)
      exit(0);
    if(p->next == NULL)
      exit(0);
    q = p->next;
    if(!q || i < 1)
      exit(0);
    p->next = q->next;
    free(q);
  }
}

打印

/* 打印所有结点 */
void TravelList(LinkList L)
{
  int j = 1;
  LNode *p = L->next;
  printf("打印：\n");
  while (p)
  {
    printf("%d---%d\n", j, p->data);
    j++;
    p = p->next;
  }
}

尾插法

/*
  尾插法：向表尾添加元素
  思路：
    1. 声明一个循环指针r，r必须指向表尾元素
    2. 循环获取输入的数据x
    3. 在循环里面声明一个新结点s
    4. 在循环里面s的data设为x
    5. 在循环里面r的next设为s
    6. 在循环里面将r向前移，即将r指向s
    7. 循环结束，r的指向的表尾元素，所以需要将r的next设置为NULL
*/
LinkList ListTailInsert(LinkList L)
{
  int x;
  InitList(&L);
  LNode *s, *r = L;
  scanf("%d", &x);
  while (x != 9999)
  {
    s = (LNode *)malloc(sizeof(LNode));
    s->data = x;
    r->next = s;
    r = s;
    scanf("%d", &x);
  }
  r->next = NULL;
  return L;
}

头插法

/*
  头插法：向表头添加元素
  思路：
    1. 循环获取输入的数据x
    2. 在循环里面声明一个新结点s
    3. 在循环里面s的data设为x
    4. 在循环里面s的next设为头结点的next
    6. 在循环里面将头结点的next设为s
*/
LinkList ListHeadInsert(LinkList L)
{
  int x;
  InitList(&L);
  LNode *s;
  scanf("%d", &x);
  while (x != 9999)
  {
    s = (LNode *)malloc(sizeof(LNode));
    s->data = x;
    s->next = L->next;
    L->next = s;
    scanf("%d", &x);
  }
  return L;
}

链表逆置

/*
  链表逆置（使用头插法）
  思路：
    1. 声明两个结点指针p, q
    2. p指向链表L的的第一个结点
    3. L的头结点的next指向NULL，相当于分离出了两个链表：p和L
    4. 使用q循环读取链表p上的结点
    5. 使用头插法把读取到的结点插入到L中
*/
void ListInverse(LinkList L)
{
  LNode *p, *q;
  p = L->next;
  L->next = NULL;
  
  while (p != NULL)
  {
    // q重置为p链表当前的结点
    q = p;
    // p继续向前移
    p = p->next;
    // 使用头插法
    q->next = L->next;
    L->next = q;
  }
}

企业链

来由

企业链也称通用链表，结点数据域的数据类型可以根据客户需求灵活设定，不需要写死

实现

• defs.h

#ifndef DEFS_H
#define DEFS_H

#include <stdlib.h>
#include <stdio.h>

// 链表小结点
typedef struct LINKNODE
{
  struct LINKNODE* next;
} LinkNode;

// 链表结点
typedef struct LINKLIST
{
  LinkNode head;
  int size;
} LinkList;

// 遍历的函数指针
typedef void(*PRINTNODE)(LinkNode*);
// 比较数据域是否相等的函数指针
typedef int(*COMPARENODE)(LinkNode*, LinkNode*);

// 初始化链表
LinkList* Init_LinkList()
{
  LinkList* list = (LinkList*)malloc(sizeof(LinkList));
  list->head.next = NULL;
  list->size = 0;
  return list;
}

// 插入
void Insert_LinkList(LinkList* list, int pos, LinkNode* data)
{
  if(list == NULL)
    return;
  if(data == NULL)
    return;
  if(pos < 0 || pos > list->size)
    pos = list->size;
  // 查找插入位置
  LinkNode* pCurrent = &(list->head);
  for (int i = 0; i < pos; i++)
  {
    pCurrent = pCurrent->next;
  }
  // 插入新节点
  data->next = pCurrent->next;
  pCurrent->next = data;

  list->size++;
}

// 删除
void Remove_LinkList(LinkList* list, int pos)
{
  if(list == NULL)
    return;
  if(pos < 0 || pos >= list->size)
    return;
  LinkNode* pCurrent = &(list->head);
  for (int i = 0; i < pos; i++)
  {
    pCurrent = pCurrent->next;
  }
  pCurrent->next = pCurrent->next->next;
  list->size--;
}

// 查找
int Find_LinkList(LinkList* list, LinkNode* data, COMPARENODE compare)
{
  if(list == NULL)
    return -1;
  if(data == NULL)
    return -1;
  LinkNode* pCurrent = list->head.next;
  int pos = -1;
  for (int i = 0; i < list->size; i++)
  {
    if(compare(pCurrent, data) == 1)
    {
      pos = i;
      break;
    }
    pCurrent = pCurrent->next;
  }
  return pos;
}

// 返回链表大小
int Size_LinkList(LinkList* list);

// 打印
void Print_LinkList(LinkList* list, PRINTNODE print)
{
  if(list == NULL)
    return;
  LinkNode* pCurrent = list->head.next;
  while (pCurrent != NULL)
  {
    print(pCurrent);
    pCurrent = pCurrent->next;
  }
  
}

// 释放链表内存
void FreeSpace_LinkList(LinkList* list)
{
  if(list == NULL)
    return;
  free(list);
}
#endif

• main.c

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "defs.h"

typedef struct PERSON
{
  LinkNode node;
  char name[64];
  int age;
}Person;

// 自定义打印函数
void MyPrint(LinkNode* data)
{
  Person* p = (Person*)data;
  printf("name:%s, age:%d\n", p->name, p->age);
}

// 自定义比较数据域函数
int MyCompare(LinkNode* data1, LinkNode* data2)
{
  Person* p1 = (Person*)data1;
  Person* p2 = (Person*)data2;
  if(p1->name == p2->name && p1->age == p2->age)
    return 1;
  else
    return 0;  
}

void main()
{
  LinkList* list = Init_LinkList();
  Person p1, p2, p3, p4, p5;
  strcpy(p1.name, "aaa");
  strcpy(p2.name, "bbb");
  strcpy(p3.name, "ccc");
  strcpy(p4.name, "ddd");
  strcpy(p5.name, "eee");
  p1.age = 10;
  p2.age = 20;
  p3.age = 30;
  p4.age = 40;
  p5.age = 50;

  Insert_LinkList(list, 0, (LinkNode*)&p1);
  Insert_LinkList(list, 1, (LinkNode*)&p2);
  Insert_LinkList(list, 2, (LinkNode*)&p3);
  Insert_LinkList(list, 3, (LinkNode*)&p4);
  Insert_LinkList(list, 4, (LinkNode*)&p5);

  Print_LinkList(list, MyPrint);

  printf("---------------\n");

  LinkNode* tmp_p = (LinkNode*)&p4;

  Remove_LinkList(list, 2);

  Print_LinkList(list, MyPrint);

  int pos = Find_LinkList(list, tmp_p, MyCompare);
  printf("find pos: %d", pos);

  FreeSpace_LinkList(list);
}

双链表（带头结点）

定义

/* 结点的结构体 */
struct LNode
{
  int data;
  struct LNode * prior;
  struct LNode *next;
};
typedef struct LNode LNode;
typedef struct LNode *LinkList;

初始化

/* 初始化链表 */
void InitDLinkList(LinkList *L)
{
  *L = (LNode *)malloc(sizeof(LNode));  // 分配一个头结点
  if(*L == NULL)
  {
    printf("分配结点失败\n");
    exit(-1);
  }
  (*L)->prior = NULL; // 头结点的prior永远指向NULL
  (*L)->next = NULL;  // 头结点之后暂时没有结点
  printf("初始化列表完成\n");
}

是否为空

/* 判断链表是否为空 */
void DLinkListEmpty(LinkList L)
{
  if(L->next == NULL)
    printf("链表为空\n");
  else
    printf("链表不为空\n");
}

后插

/* 
  后插
  思路：
    1. 生成新结点s，s的data设为e
    2. s结点的next指向p的next
    3. p的next的prior指向s（此时s和s下一个结点的互指已完成）
    4. s的prior指向p
    5. p的next指向s（最后完成p和s的互指）
*/
int InsertNextNode(LNode *p, int e)
{
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));
  s->data = e;
  s->next = p->next;
  if(p->next != NULL)
    p->next->prior = s;
  s->prior = p;
  p->next = s;
  return 0;
}

前插

/* 
  指定结点的前插
  思路：
    1. 声明一个新节点s
    2. s的next设为指定结点的next
    3. 指定结点p的next的prior指向s（完成s与p-next结点的互指）
    4. s的prior指向指定结点p
    5. 指定结点p的next指向s（完成s与p的互指）
    4. s的data设为p的data
    5. p的data设为e
*/
int InsertPriorNode(LNode *p, int e)
{
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));
  s->next = p->next;
  if(p->next != NULL)
    p->next->prior = s;
  s->prior = p;
  p->next = s;
  s->data = p->data;
  p->data = e;
  return 0;
}

删除

/*
  删除p结点的后继结点
  思路：
    1. 令q = p的next，即q为p的后继结点
    2. 完成q的next和p的互指
    3. 释放q结点
*/
int DeleteNextNode(LNode *p)
{
  if(p == NULL)
    exit(0);
  LNode *q = p->next;
  if(q == NULL)
    exit(0);
  p->next = q->next;
  if(q->next != NULL)
    q->next->prior = p;
  free(q);
  return 0;
}

打印

/* 打印所有结点 */
void TravelList(LinkList L)
{
  int j = 1;
  LNode *p = L->next;
  printf("打印：\n");
  while (p)
  {
    printf("%d---%d\n", j, p->data);
    j++;
    p = p->next;
  }
}

循环单链表（带头结点）

概念

• 表尾结点的next指向头结点

定义

/* 结点的结构体 */
struct LNode
{
  int data;
  struct LNode *next;
};
typedef struct LNode LNode;
typedef struct LNode *LinkList;

初始化

/* 初始化链表 */
void InitCLinkList(LinkList *L)
{
  *L = (LNode *)malloc(sizeof(LNode));  // 分配一个头结点
  if(*L == NULL)
  {
    printf("分配结点失败\n");
    exit(-1);
  }
  (*L)->next = *L;  // 头结点的next指回头结点
  printf("初始化列表完成\n");
}

是否为空

/* 判断链表是否为空 */
void CLinkListEmpty(LinkList L)
{
  // 这里判断结点的next是否指向头结点，不是==NULL，注意区分
  if(L->next == L)
    printf("链表为空\n");
  else
    printf("链表不为空\n");
}

获取长度

/* 获取链表长度 */
int CLinkListLength(LinkList L)
{
  int j = 0;
  LNode *p = L->next;
  while (p != L)
  {
    j++;
    p = p->next;
  }
  printf("链表的长度是%d\n", j);
  return j;
}

打印

/* 打印所有结点 */
void TravelList(LinkList L)
{
  int j = 1;
  LNode *p = L->next;
  printf("打印：\n");
  while (p != L)
  {
    printf("%d---%d\n", j, p->data);
    j++;
    p = p->next;
  }
}

循环双链表（带头结点）

概念

• 表尾结点的next指向头结点
• 头结点的prior指向表尾结点

定义

/* 结点的结构体 */
struct LNode
{
  int data;
  struct LNode *next;
  struct LNode *prior;
};
typedef struct LNode LNode;
typedef struct LNode *LinkList;

初始化

/* 初始化链表 */
void InitCDLinkList(LinkList *L)
{
  *L = (LNode *)malloc(sizeof(LNode));  // 分配一个头结点
  if(*L == NULL)
  {
    printf("分配结点失败\n");
    exit(-1);
  }
  (*L)->next = *L;  // 头结点的next指回头结点
  (*L)->prior = *L;  // 头结点的prior指回头结点
  printf("初始化列表完成\n");
}

是否为空

/* 判断链表是否为空 */
void CDLinkListEmpty(LinkList L)
{
  // 这里判断结点的next是否指向头结点，不是==NULL，注意区分
  if(L->next == L)
    printf("链表为空\n");
  else
    printf("链表不为空\n");
}

获取长度

/* 获取链表长度 */
int CDLinkListLength(LinkList L)
{
  int j = 0;
  LNode *p = L->next;
  while (p != L)
  {
    j++;
    p = p->next;
  }
  printf("链表的长度是%d\n", j);
  return j;
}

后插

/* 
  后插（与单链表不同的是不用判断p的next是否为空）
  思路：
    1. 生成新结点s，s的data设为e
    2. s结点的next指向p的next
    3. p的next的prior指向s（此时s和s下一个结点的互指已完成）
    4. s的prior指向p
    5. p的next指向s（最后完成p和s的互指）
*/
int InsertNextNode(LNode *p, int e)
{
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));
  s->data = e;
  s->next = p->next;
  p->next->prior = s;
  s->prior = p;
  p->next = s;
  return 0;
}

前插

/* 
  指定结点的前插（先后插，再互换data）
  思路：
    1. 声明一个新节点s
    2. s的next设为指定结点的next
    3. 指定结点p的next的prior指向s（完成s与p-next结点的互指）
    4. s的prior指向指定结点p
    5. 指定结点p的next指向s（完成s与p的互指）
    4. s的data设为p的data
    5. p的data设为e
*/
int InsertPriorNode(LNode *p, int e)
{
  if(p == NULL)
    exit(-1);
  LNode *s = (LNode *)malloc(sizeof(LNode));
  s->next = p->next;
  p->next->prior = s;
  s->prior = p;
  p->next = s;
  s->data = p->data;
  p->data = e;
  return 0;
}

打印

/* 打印所有结点 */
void TravelList(LinkList L)
{
  int j = 1;
  LNode *p = L->next;
  printf("打印：\n");
  while (p != L)
  {
    printf("%d---%d\n", j, p->data);
    j++;
    p = p->next;
  }
}

静态链表

概念

• 用数据的方式实现的链表
• 分配一整片连续的内存空间，各个结点集中安置
• 单链表的区别，静态链表的next指向的是下一个结点的数组下标（游标），单链表指向的是地址
• 初始化的时候空数据设为-2，尾结点的next设为-1
• 优点：增删操作不需要大量移动元素
• 缺点：不能随机存取，只能从头结点开始依次往后查找，容量固定不变

定义

#define MaxSize 10

/* 结点的结构体 */
struct LNode
{
  int data;
  int next;
};
typedef struct LNode SLinkList[MaxSize];

顺序表和链表的对比

1. 逻辑结构
   • 都属于线性表
2. 物理结构
   • 顺序表支持随机存取，存储密度高
   • 顺序表大片连续空间分配不方便，改变容量不容易
   • 链表离散的小空间分配方便，改变容量方便
   • 链表不可随机存取，存储密度低
3. 基本操作
   • 初始化
     • 顺序表需要分配大片连续空间，若分配空间过小，不方便扩展容量，分配空间过大，则浪费内存空间
     • 链表只需分配一个头结点或头指针，之后方便扩展
   • 销毁
     • 顺序表的销毁可以先把length=0，如果顺序表是通过静态分配创建的，系统会自动回收空间，如果是动态分配方式（malloc）创建的，需要手动free掉
     • 链表的销毁顺序依次free各个结点
   • 插入和删除
     • 顺序表在插入或删除都需要将元素前移或后移，移动元素的时间复杂度是O（n），若数据元素很大，则移动的时间代价很高
     • 链表的插入或删除只需修改指针即可，不需要直接移动元素
   • 查找
     • 顺序表的按位查找：O（1），链表的按位查找：O（n）
     • 顺序表的按值查找：O（），链表的按值查找：O（n）
4. 应用场景
   • 表长难以估计，经常要增加/删除元素 ——链表
   • 表长可估计，经常需要查询操作 ——顺序表